合成加速度ってなに？

実際の加速度と計測される加速度の違い

落下試験では、物体に発生する加速度を、加速度ピックアップ（加速度センサ）で数値化します。通常、加速度ピックアップは並進運動（一直線上の運動）を計測するセンサが用いられ、その軸（加速度を計測する方向）は３軸（上下、前後、左右）となります。
ここでは、並進３軸の加速度成分から計算される、合成加速度について解説していきます。

物体が落下して床面に衝突すると、物体には加速度が発生します（詳細はこちら）
このとき、物体がまっすぐに床面と衝突した場合と、傾いて衝突した場合において、発生する加速度は図1のように異なります。下図では説明を簡単にするため、物体の傾きに関係なく、発生する加速度の大きさを同一と見なし、加速度ピックアップにてその大きさを計測したとします。

いま、物体に傾きが無い状態で落下した物体に発生する加速度は、実際に発生した加速度がそのまま記録されます。一方で物体が傾いた状態で落下した場合には、実際に発生する加速度はそのまま記録されず、その傾きに応じて、それぞれの軸に加速度が分散し、それが記録されます。

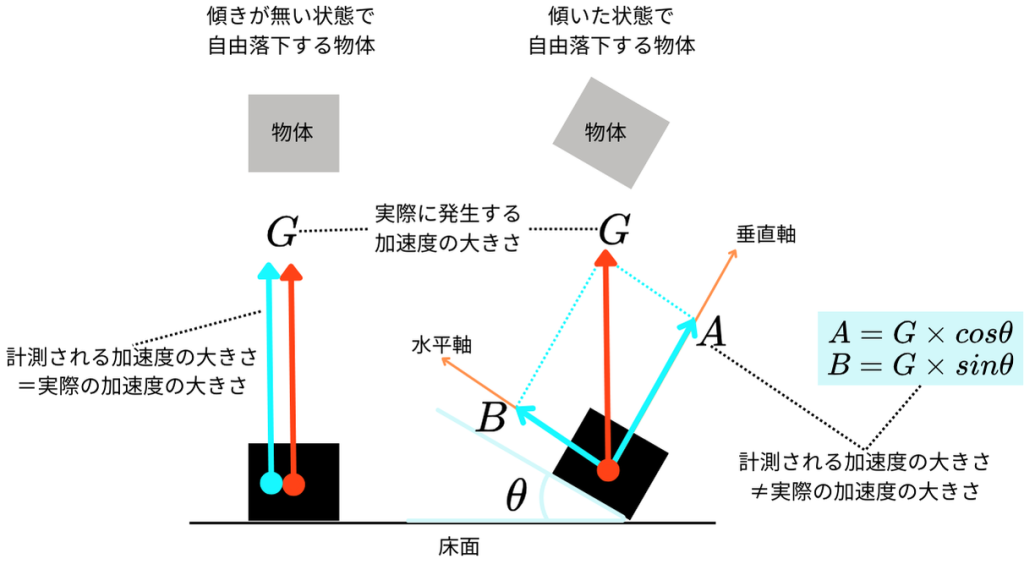
ここでたとえば、実際に発生した加速度G（図1の赤い矢印）を100Gとし、物体の角度（図1のθ）が30°であったとすると、計測される加速度Aと加速度Bの大きさはそれぞれ、以下のようになります。

A＝100×cos30°=86.6G
B=100×sin30°=50.0G

ここでは、実際に100Gが発生しているにもかかわらず、Aの計測値は86.6Gとなりました。このように一般的に、物体が傾いて落下すると、記録される加速度は計算上、実際に発生する加速度よりも小さくなります。したがって、角度が付いた状態で記録された加速度を見て設計の合否判定を行うと、誤った判断を行うリスクが考えられます。

合成加速度の計算方法

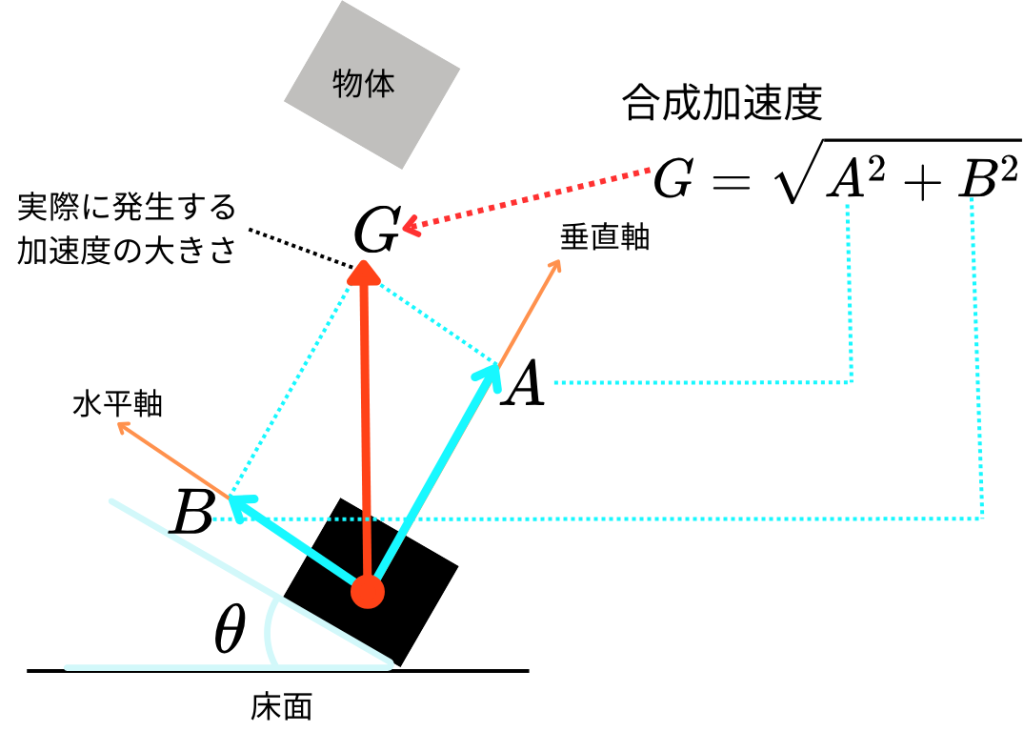
合成加速度とは、本来発生した加速度の大きさのことで、物体の傾きによって分散した加速度を合成することで求めることができます。図2では、2方向の軸に分散した数値のみを利用した場合の計算式です。３軸センサの場合には、さらにもう1軸の測定結果を加えることで、物体の３次元的な傾きを考慮した合成加速度が計算できます。

たとえば下記の計算結果から、合成加速度Gを計算してみると、実際に発生した加速度（100G)と同一の結果が得られます。
A＝100×cos30°=86.6G
B=100×sin30°=50.0G
G=（86.6^2+50.0^2)^0.5=100G

これまで解説したように、合成加速度を用いれば、実際に発生した加速度を求めることで、より適切な指標となります。（ただし、ここでは便宜上、物体に傾きがある状態と、傾きが無い状態において、発生する加速度は同一と仮定して解説しましたが、実際の落下では傾くことで、物体の挙動も変化するため、傾きが無い状態と傾きがある場合で発生する最大加速度は異なることに注意が必要です）
このような落下の傾きで生じる「ばらつき」をできるだけ少なくするために、落下試験機を用いた落下試験の実施が実用化されています。（詳細はこちら）

合成加速度は３軸成分の加速度があれば表計算ソフトでも計算できますが、正確な合成加速度を求めるためには、加速度計測のちょっとしたコツが必要です。このコツをお知りになりたい方は、是非資料をダウンロードしてご確認をお願いします。

参考までに、自動的に合成加速度を計算させたい場合には、衝撃加速度計測システム（ショックマネージャ）の専用ソフトウェアに合成加速度表示機能が搭載されています。

資料ダウンロード

合成加速度に関する資料が欲しい方は下記から登録をお願いします。